Mastering Trigonometry for GCSE Maths is a critical skill for students aiming for top grades in their exams. Trigonometry plays a major role in solving problems related to angles, triangles, and real-world applications such as engineering, physics, and navigation.
If you find trigonometry challenging, don’t worry. With the right approach, structured revision, and practice, you can develop a strong understanding of trigonometric concepts and apply them effectively in your GCSE Maths exam.
This guide provides 10 proven strategies to help you master trigonometry and confidently tackle any exam question.
Why Mastering Trigonometry for GCSE Maths is Essential
Trigonometry is one of the most tested topics in GCSE Maths, and here’s why you need to master it:
✔ Strong Exam Weighting: A significant number of GCSE Maths questions involve trigonometry.
✔ Foundation for Advanced Maths: Trigonometry is essential for learning calculus, physics, and geometry.
✔ Real-World Applications: Used in engineering, navigation, construction, and astronomy.
🔗 Related Guide: GCSE Maths Revision Tips: Study Smarter, Not Harder
10 Proven Strategies for Mastering Trigonometry for GCSE Maths
1. Understand the Basics of Trigonometry
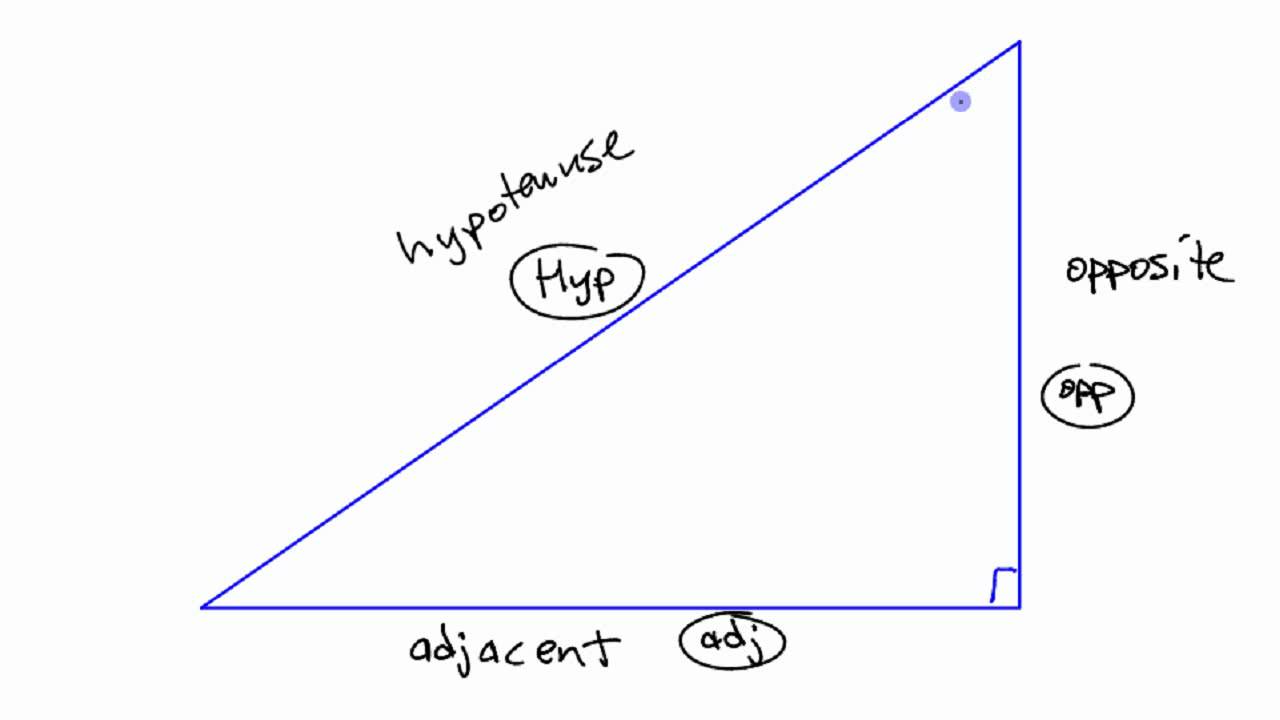
Before solving complex problems, ensure you have a solid understanding of right-angled triangles and their components:
✔ Opposite Side: The side opposite the given angle.
✔ Adjacent Side: The side next to the angle, but not the hypotenuse.
✔ Hypotenuse: The longest side in a right-angled triangle.
📌 Action Step:
✔ Label the sides correctly before applying trigonometric ratios.
🔗 Related Guide: Essential GCSE Maths Formulas You Must Know
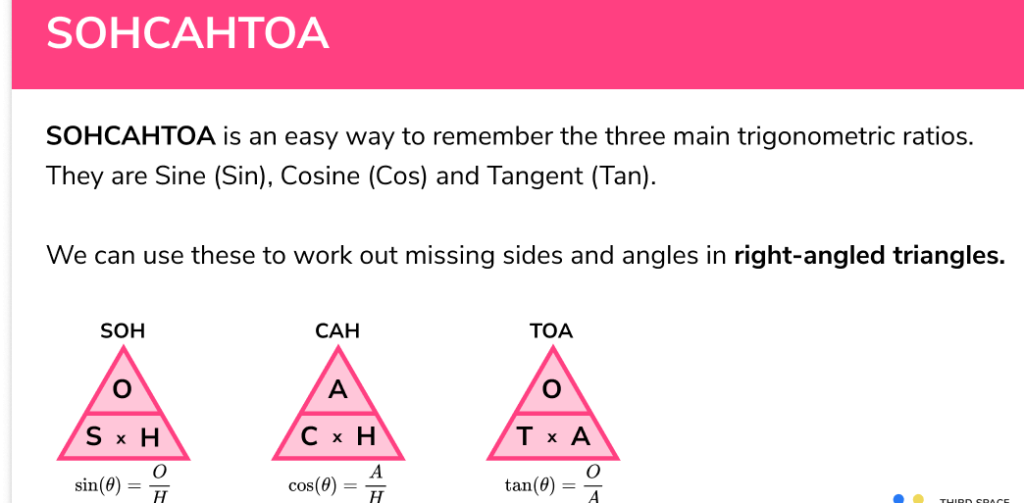
2. Learn and Memorize the Trigonometric Ratios
The three primary trigonometric ratios are:
✔ Sine: sin(θ)=OppositeHypotenuse\sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}
✔ Cosine: cos(θ)=AdjacentHypotenuse\cos(\theta) = \frac{\text{Adjacent}}{\text{Hypotenuse}}
✔ Tangent: tan(θ)=OppositeAdjacent\tan(\theta) = \frac{\text{Opposite}}{\text{Adjacent}}
📌 Action Step:
✔ Use the SOHCAHTOA mnemonic to memorize these ratios.
🔗 Related Guide: Mastering GCSE Maths Trigonometric Ratios
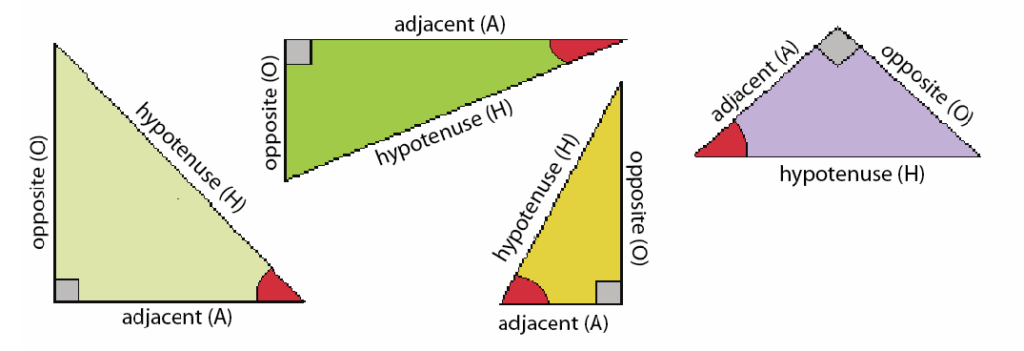
3. Practice Identifying Triangle Sides
Many students struggle with correctly identifying the opposite, adjacent, and hypotenuse sides.
📌 Action Step:
✔ Work through at least 10 practice problems identifying triangle sides before applying trigonometric formulas.
4. Learn to Use a Calculator for Trigonometric Ratios
Trigonometry questions often require finding sine, cosine, and tangent values using a calculator.
📌 Action Step:
✔ Practice using scientific calculators to solve for missing sides and angles.
🔗 Related Guide: Using Calculators Effectively for GCSE Maths
5. Solve for Missing Sides in Right-Angled Triangles
Many GCSE trigonometry questions require you to find unknown sides in a right-angled triangle.
Example:
Find the opposite side if θ=30∘\theta = 30^\circ and the hypotenuse is 10 cm
sin(30∘) = Opposite/10
Opposite=10×sin(30∘)=5 cm
📌 Action Step:
✔ Solve 5-10 similar problems daily to build confidence.
6. Solve for Missing Angles Using Inverse Trigonometry
To find a missing angle, use inverse trigonometric functions:
Example:
If opposite = 5 cm and hypotenuse = 10 cm, find θ\theta:
sin(θ)=510=0.5\sin(\theta) = \frac{5}{10} = 0.5 θ=sin−1(0.5)=30∘\theta = \sin^{-1}(0.5) = 30^\circ
📌 Action Step:
✔ Practice using sin⁻¹, cos⁻¹, and tan⁻¹ to find missing angles.
7. Master the Sine Rule and Cosine Rule
For non-right-angled triangles, you’ll need these formulas:
✔ Sine Rule:
asinA=bsinB=csinC\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}✔ Cosine Rule:
c2=a2+b2−2abcosCc^2 = a^2 + b^2 - 2ab \cos C📌 Action Step:
✔ Use these rules to solve problems involving non-right-angled triangles.
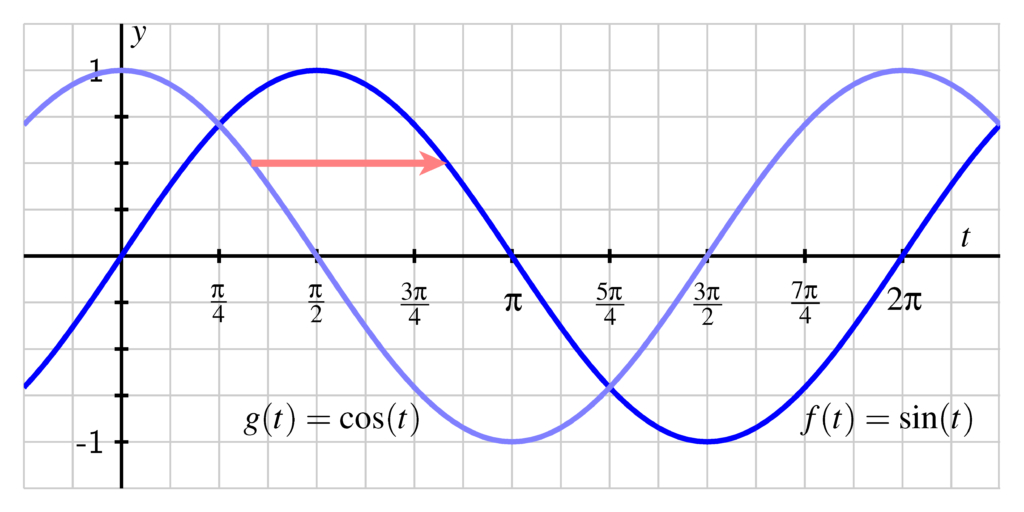
8. Understand and Sketch Trigonometric Graphs
You may be asked to interpret sine, cosine, and tangent graphs in your exam.
📌 Action Step:
✔ Practice sketching and identifying key properties of these graphs, including their period and amplitude.
🔗 Related Guide: Graphing Trigonometric Functions for GCSE Maths
9. Apply Trigonometry to Real-World Problems
A GCSE Maths tutor can provide one-on-one guidance to strengthen weak areas and boost confidence.
📌 Action Step:
✔ Find an experienced tutor on MathZem.com for personalized support.
🔗 Related Guide: How a GCSE Maths Tutor Can Improve Your Grades
10. Get Extra Help from a GCSE Maths Tutor
If you’re struggling with certain trigonometry concepts, a GCSE Maths tutor can provide personalized guidance.
📌 Action Step:
✔ Find an experienced tutor on MathZem.com for one-on-one support.
🔗 Related Guide: Why a GCSE Maths Tutor Can Improve Your Grades
FAQs About Mastering Trigonometry for GCSE Maths
✔ What’s the best way to memorize trigonometric ratios?
Use SOHCAHTOA, practice problems, and apply the ratios in real-world contexts.
✔ How do I solve problems involving non-right-angled triangles?
Use the sine rule and cosine rule for solving complex triangles.
✔ Can I use a calculator for trigonometry?
Yes, but you should also practice solving problems manually.
✔ What if I get stuck on a problem?
Break it down into smaller steps or seek help from a GCSE Maths tutor.
Final Thoughts: Your Path to Mastering Trigonometry For GCSE Maths
Mastering Trigonometry for GCSE Maths requires practice, memorization of key formulas, and application in different problems. By following these 10 proven strategies, you’ll gain the confidence and skills needed to tackle trigonometry questions successfully.
📌 Ready to master trigonometry for your GCSE Maths exam?
🔗 Visit MathZem.com for expert tutorials, practice questions, and top GCSE Maths tutors. 🚀