Mastering Percentages for GCSE Maths
Mastering percentages for GCSE Maths is essential for tackling real-world problems and securing high marks in your exams. Percentages appear in various topics, such as finance, ratios, statistics, and probability, making them one of the most tested concepts in GCSE Maths.
With the right techniques and consistent practice, you can quickly and accurately calculate percentages in exam questions and everyday life.
This guide will provide 10 expert strategies to help you master percentages for GCSE Maths and boost your confidence before exam day.
Why Mastering Percentages for GCSE Maths is Important
Percentages play a crucial role in GCSE Maths because they are widely used in both academic and real-life applications. Here’s why mastering percentages is important:
✔ Essential for Exams – Percentage problems appear frequently in GCSE Maths exams.
✔ Practical in Daily Life – Used in discounts, interest rates, and tax calculations.
✔ Foundation for Advanced Maths – Essential for understanding ratios, probability, and proportions.
🔗 Related Guide: GCSE Maths Revision Tips: Study Smarter, Not Harder
10 Proven Strategies for Mastering Percentages for GCSE Maths
1. Understand the Basics of Percentages
A percentage represents a fraction of 100. For example:
✔ 50% means 50/100 0r 1/2
✔ 25% means 25/100 or 1/4
📌 Action Step:
✔ Learn how to express percentages as fractions and decimals.
🔗 Related Guide: Essential GCSE Maths Formulas You Must Know
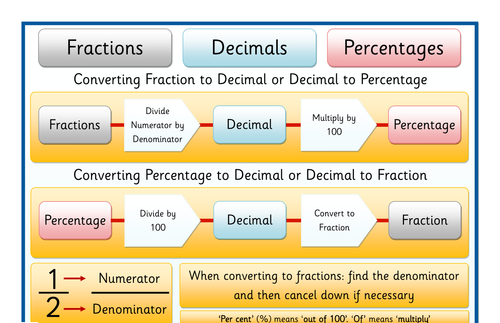
2. Convert Between Percentages, Fractions, and Decimals
Understanding how to convert between percentages, decimals, and fractions is crucial for solving exam problems efficiently.
Examples:
✔ Convert 25% to a decimal → 0.25
✔ Convert 25% to a fraction → 25/100 = 1/4
✔ Convert 0.75 to a percentage → 75
📌 Action Step:
✔ Practice converting percentages, decimals, and fractions using flashcards.
3. Calculate Percentages of a Number
Use this formula to find a percentage of a given number:
Percentage of a quantity = Percentage/100 × Quantity
Example:
Find 20% of 150:
20/100 x 150 = 30
📌 Action Step:
✔ Solve 10+ practice problems calculating percentages of different values.

4. Find the Original Amount After a Percentage Change
If given a final amount after a percentage increase or decrease, you can work backward to find the original value.
Example:
If £120 is 20% more than the original amount, find the original amount:
Original Amount = 120/1.20 = 100
📌 Action Step:
✔ Practice reverse percentage calculations to strengthen your understanding.

5. Calculate Percentage Increase and Decrease
Use this formula to calculate percentage change:
Percentage Change = New Value − Original Value / Original Value X 100
Example:
If the price of a product increases from £50 to £60, the percentage increase is:
60 - 50 / 50 X 100 = 20%
📌 Action Step:
✔ Solve real-world percentage change problems, such as price increases and salary raises.
6. Solve Multi-Step Percentage Problems
Some GCSE Maths questions require multiple percentage calculations in a single problem.
Example:
A shirt costs £40 after a 20% discount. Find the original price:
Original price = 40 / 0.80 = 50
📌 Action Step:
✔ Practice real-world word problems involving percentages.
🔗 Related Guide: How to Solve GCSE Maths Word Problems Effectively
7. Master Compound Interest Calculations
Compound interest is commonly tested in GCSE Maths and is used in finance.
A = P (1+100/r)^n
✔ AAA = Final amount
✔ PPP = Principal (initial) amount
✔ rrr = Interest rate
✔ nnn = Number of years
Example:
Calculate the final amount if £1000 is invested at 5% compound interest for 2 years:
A = 1000(1+5/100)^2 = £1102.50
A = £1102.50
📌 Action Step:
✔ Solve compound interest problems using the formula.

8. Apply Percentages to Real-World Problems
Percentages are widely used in finance, business, and statistics.
Examples:
✔ Calculate VAT, sales tax, and tips.
✔ Find discounted prices during sales.
📌 Action Step:
✔ Apply percentages to real-world financial scenarios.
🔗 Related Guide: GCSE Maths in Real Life: Everyday Applications
9. Use Online Tools and Interactive Resources
Many online resources provide interactive exercises, quizzes, and practice tests.
📌 Action Step:
✔ Explore MathZem.com, Khan Academy, and Corbett Maths for video tutorials and quizzes.
10. Seek Help from a GCSE Maths Tutor
If percentages still feel challenging, a GCSE Maths tutor can provide:
✔ One-on-one guidance on tricky topics.
✔ Step-by-step problem-solving techniques.
✔ Targeted exam preparation for higher grades.
📌 Action Step:
✔ Find an experienced tutor on MathZem.com to master percentages for GCSE Maths.
🔗 Related Guide: Why a GCSE Maths Tutor Can Improve Your Grades
FAQs About Mastering Percentages for GCSE Maths
1. What’s the best way to memorize percentage formulas?
Use flashcards, write them down repeatedly, and practice them in real-world problems such as shopping discounts and interest calculations.
2. How do I solve problems involving percentage change?
Apply the percentage change formula:
Percentage Change = New Value−Original Value / Original Value X 100
3. Can I use a calculator for percentages in GCSE Maths?
Yes, calculators are allowed for some percentage problems, but you should also practice solving them manually to improve speed and accuracy.
4. What should I do if I struggle with percentage word problems?
Break the problem into smaller steps, identify key values, and use the appropriate formula. If needed, seek help from a GCSE Maths tutor for additional guidance.
Final Thoughts: Your Path to Mastering Trigonometry For GCSE Maths
Mastering percentages is a key skill for GCSE Maths, essential for exam success and real-world applications. With consistent practice, strategic learning techniques, and the right resources, you can tackle percentage-based questions with ease.
📌 Need extra help? Visit MathZem.com for expert tutorials, practice questions, and one-on-one tutoring sessions tailored to GCSE Maths success. 🚀