Algebra is a fundamental skill in GCSE Maths, appearing in almost every exam paper. It forms the foundation for many advanced topics, including equations, graphs, and functions. While algebra can seem challenging at first, with the right approach and consistent practice, you can master it and significantly improve your GCSE Maths score.
In this guide, we’ll explore 10 powerful strategies to help you understand algebra, apply key formulas, and solve equations with confidence.
Why Mastering Algebra for GCSE Maths is Crucial for Exam Success
Algebra is one of the most heavily tested areas in GCSE Maths. Here’s why it’s essential:
✔ Foundation for Advanced Math: Algebra is crucial for understanding topics like trigonometry, geometry, and calculus.
✔ Problem-Solving Skills: Algebra enhances logical thinking and analytical reasoning.
✔ High Exam Weighting: A significant portion of the GCSE Maths exam involves algebra-based questions.
🔗 Related Guide: GCSE Maths Revision Tips: Study Smarter, Not Harder
10 Strategies for Mastering Algebra for GCSE Maths
1. Understand the Core Concepts of Algebra
Before diving into complex algebra, make sure you understand the fundamental concepts:
✔ Variables: Symbols (e.g., x, y) representing unknown numbers.
✔ Expressions: mathematical statements without an equals sign (e.g., 3x + 5).
✔ Equations: Statements with an equals sign that can be solved (e.g., 2x + 3 = 7).
📌 Action Step:
✔ Revise basic algebraic operations like simplifying expressions and solving simple equations.
🔗 Related Guide: Essential Maths Formulas for GCSE Exams
Memorize Key Algebra Formulas for GCSE Maths
Certain algebra formulas are essential for GCSE math. You’ll need to memorize and apply them regularly.
Key algebra formulas:
✔ Quadratic Formula:
x=2a−b±b2−4ac
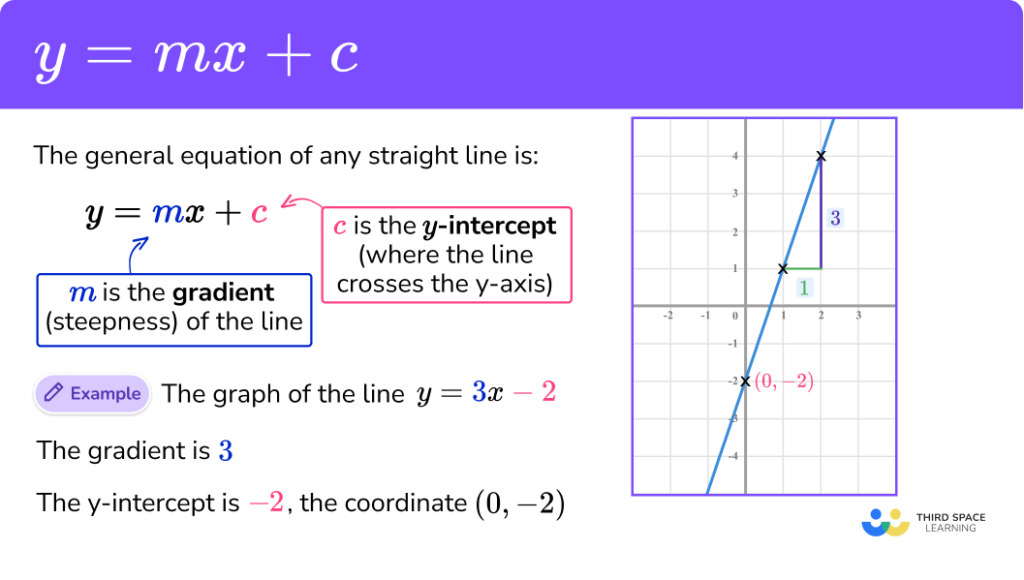
✔ Linear Equations (Slope-Intercept Form):
y=mx+c
✔ Laws of Indices:
a^m x a^n = a^m+n
📌 Action Step:
✔ Create a formula sheet and review it daily.
✔ Practice applying each formula to real exam questions.
🔗 Related Guide: Mastering Quadratic Equations for GCSE Maths
3. Practice Solving Equations Daily
Solving algebraic equations is one of the most important skills for GCSE math.
Example:
Solve
3x + 5 = 20:
✔ Step 1: Subtract 5 from both sides → 3x = 15
✔ Step 2: Divide by 3 → x = 5
📌 Action Step:
✔ Practice solving linear, quadratic, and simultaneous equations daily.
✔ Use past GCSE Math papers to apply these skills in real exam conditions.
🔗 Related Guide: Best Online Resources for GCSE Maths Practice
4. Master Factorization Techniques
Factorization helps simplify expressions and solve quadratic equations efficiently.
Example: Factorize
x² + 5x + 6
✔ Step 1: Find two numbers that multiply to 6 and add to 5 (2 and 3).
✔ Step 2: Rewrite: (x + 2)(x + 3).
📌 Action Step:
✔ Practice factorizing quadratic expressions and applying the difference of squares method.
5. Understand and Solve Inequalities
Inequalities are similar to equations but use <, >, ≤, and ≥ instead of =.
Example: Solve 2x + 3 < 7
✔ Step 1: Subtract 3 from both sides → 2x < 4
✔ Step 2: Divide by 2 → x < 2
📌 Action Step:
✔ Practice graphing inequalities and solving real-life inequality problems.
6. Work with Algebraic Graphs
Understanding graphs helps visualize equations and functions.
Key Graph Types:
✔ Linear Graphs: y = mx + c (straight lines).
✔ Quadratic Graphs: y = ax² + bx + c (parabolas).
📌 Action Step:
✔ Plot graphs manually and using graphing tools like Desmos.
✔ Learn how to interpret gradients, intercepts, and turning points.
🔗 Related Guide: Understanding Graphs in GCSE Maths
7. Solve Algebra Word Problems
Word problems test real-world applications of algebra.
Example:
“A number increased by 5 is equal to 12. Find the number.”
✔ Step 1: Define variable → x + 5 = 12
✔ Step 2: Solve for x → x = 7
📌 Action Step:
✔ Convert real-life scenarios into algebraic equations.
✔ Practice word problems from past GCSE Maths papers
8. Use Online Resources for Extra Practice
Online platforms provide interactive lessons, practice questions, and video tutorials.
📌 Best Online Resources:
✔ MathZem.com: Expert tutorials and GCSE Maths revision.
✔ Khan Academy: Free algebra video lessons.
✔ Corbett Maths: Step-by-step algebra worksheets
9. Get Extra Support from a GCSE Maths Tutor
A GCSE Maths tutor can provide one-on-one guidance to strengthen weak areas and boost confidence.
📌 Action Step:
✔ Find an experienced tutor on MathZem.com for personalized support.
🔗 Related Guide: How a GCSE Maths Tutor Can Improve Your Grades
10. Practice, Revise, and Review Regularly
Consistent revision and practice are the keys to mastering algebra for GCSE Maths.
📌 Action Step:
✔ Solve at least 10 algebra problems daily.
✔ Review mistakes and learn from them.
✔ Take mock exams under timed conditions.
🔗 Related Guide: Why Practice Papers Are Essential for GCSE Maths
FAQs About Mastering Algebra for GCSE Maths
1. What’s the best way to memorize algebra formulas?
✔ Use flashcards, write them repeatedly, and apply them in practice questions.
2. How do I solve quadratic equations?
✔ Use factorization, completing the square, or the quadratic formula.
3. Can I use a calculator for algebra?
✔ Some algebra problems require a calculator, but many (especially in Paper 1) do not.
4. What if I get stuck on a problem?
✔ Break it down into smaller steps or seek help from a GCSE Maths tutor.
Final Thoughts: Your Path to Algebra Mastery
Mastering algebra for GCSE Maths is achievable with consistent practice and the right resources. Focus on key formulas, solving equations, and applying algebra to real-world problems.
📌 Ready to master algebra and ace your GCSE Maths exams?
🔗 Visit MathZem.com for expert tutorials, practice questions, and top GCSE Maths tutors.