Geometry is one of the foundational branches of mathematics that explores shapes, sizes, dimensions, and spatial relationships. Mastering geometry fundamentals is essential for solving complex mathematical problems and understanding patterns in the world around us. Whether you’re preparing for an exam, diving into geometry for fun, or applying it to real-world challenges, this guide covers all the key concepts you need to succeed.
Let’s break down the essential geometry fundamentals, including concepts, theorems, and problem-solving techniques that will enhance your mathematical skills.
What Are Geometry Fundamentals?
Geometry fundamentals refer to the essential building blocks of geometry, such as points, lines, angles, shapes, and formulas for calculating areas, perimeters, and volumes. These concepts form the foundation of plane and solid geometry.
Key Geometry Fundamentals You Must Know
Geometry fundamentals refer to the essential building blocks of geometry, such as points, lines, angles, shapes, and formulas for calculating areas, perimeters, and volumes. These concepts form the foundation of plane and solid geometry.
1. Points, Lines, and Planes
Understanding points, lines, and planes is a crucial part of geometry fundamentals:
- Point: A location in space without any dimension
- Line: A straight path that extends infinitely in both directions
- Plane: A flat, two-dimensional surface that extends infinitely
Examples:
- A line segment has two endpoints
- A ray starts at one endpoint and extends infinitely
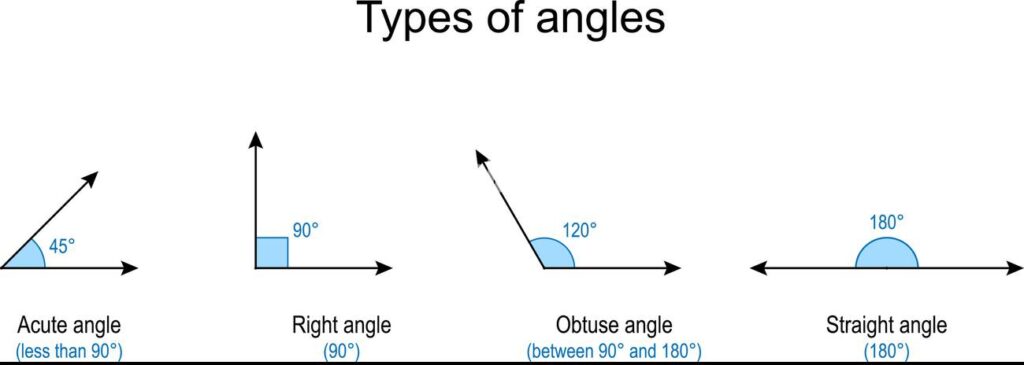
2. Types of Angles
Angles are formed when two lines intersect. Understanding different types of angles is a key part of mastering geometry fundamentals:
- Acute Angle: Less than 90°
- Right Angle: Exactly 90°
- Obtuse Angle: Between 90° and 180°
- Straight Angle: Exactly 180°
Example: In any triangle, the sum of all interior angles is always 180°.
3. Shapes and Their Properties
One of the core geometry fundamentals is understanding the properties of shapes, including polygons and circles.
- Triangles: Three sides and three angles; types include equilateral, isosceles, and scalene
- Quadrilaterals: Four-sided shapes like squares, rectangles, and parallelograms
- Circles: Defined by a radius, diameter, and circumference
Key Formula Example:
The area of a rectangle is calculated as:
Area = Length × Width
4. The Pythagorean Theorem
One of the most famous geometry fundamentals, applicable to right-angled triangles:
a² + b² = c²
Where:
aandbare the lengths of the two shorter sidescis the hypotenuse
Example:
If a = 3 and b = 4:
c² = 3² + 4² = 9 + 16 = 25 ⇒ c = 5
5. Area and Perimeter of Shapes
Understanding how to calculate the area and perimeter of different shapes is a key component of geometry fundamentals:
- Area: The space inside a shape
- Perimeter: The total distance around a shape
Examples:
- Area of a Triangle: 12×Base×Height\frac{1}{2} \times Base \times Height
- Perimeter of a Rectangle: 2×(Length+Width)2 \times (Length + Width)
6. Volume and Surface Area of 3D Shapes
3D geometry fundamental involve calculating the space inside and the total surface area of 3D objects:
- Volume: The amount of space an object occupies
- Surface Area: The total area of all faces of a 3D object
Examples:
- Volume of a Cube:
Side3Side^3 - Surface Area of a Sphere:
4πr24\pi r^2
How to Solve Geometry Problems
To effectively apply geometry fundamental, follow these steps:
- Understand the Problem: Carefully read and identify what’s being asked
- Draw a Diagram: Visualize the problem with labeled shapes and dimensions
- Apply Relevant Formulas: Use formulas for area, perimeter, or volume
- Check Your Work: Double-check calculations for accuracy
Example Problem:
Find the area of a circle with a radius of 5 cm.
Solution:
Area = πr2=π×52=25πcm2\pi r^2 = \pi \times 5^2 = 25\pi cm^2
Real-World Applications of Geometry Fundamentals
Geometry fundamental are used in a wide variety of fields:
- Architecture: Designing buildings and structures
- Engineering: Building bridges, machines, and transportation systems
- Art: Creating accurate proportions and perspectives
- Nature: Understanding patterns like honeycombs and flower petals
Tips for Mastering Geometry Fundamental
- Practice Daily: Regular problem-solving builds confidence
- Use Visual Aids: Draw diagrams to simplify complex problems
- Memorize Key Formulas: Keep a reference sheet handy
- Collaborate with Others: Study groups can enhance understanding
- Explore Online Resources: Use platforms like Mathzem Geometry Guides for interactive tools
FAQs About Geometry Fundamental
Why are geometry fundamental important?
They provide the foundation for solving complex problems and understanding spatial relationships.What’s the most challenging part of geometry fundamental?
Many students find 3D geometry and proofs difficult, but regular practice helps.How can I improve my geometry skills?
Solve problems daily, visualize shapes, and seek guidance when needed.Are there fun ways to learn geometry fundamental?
Yes! Try puzzles, geometry games, or real-world projects like designing a garden.
Final Thoughts
Mastering geometry unlocks a deeper understanding of mathematics and the world around you. By practicing consistently and applying problem-solving strategies, you can develop strong skills that will benefit you academically and beyond.